Introduction to Ratio and Proportion

Ratio and Proportion

Ratio and Proportion are important concepts in mathematics that are used to compare quantities and establish relationships between them. These concepts help in solving problems related to sharing, scaling, and comparing two or more quantities.

2. What is a Ratio?

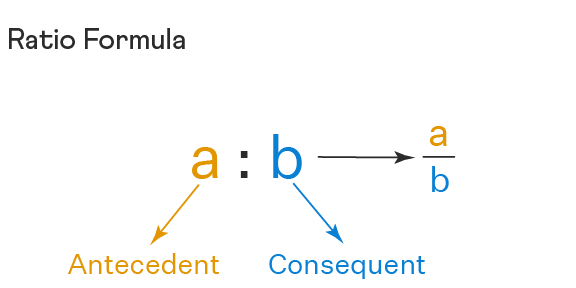
• A ratio is a way to compare two quantities of the same kind using division.
• It tells us how many times one quantity is compared to another.
• The ratio of two numbers is expressed using the symbol “:” (colon).

Example: If there are 6 boys and 4 girls in a class, the ratio of boys to girls is written as 6:4 or simplified as 3:2.

Key Points About Ratio: Ratio and Proportion

1. Ratios are written in their simplest form (like fractions).
2. Order of terms in a ratio is very important. 6:4 is not the same as 4:6.
3. Ratios have no units because they compare quantities of the same type.
4. Ratios can be scaled up or down by multiplying or dividing both terms by the same number.

3. Simplification of Ratios

To simplify a ratio, divide both terms of the ratio by their greatest common factor (GCF).

Example: Simplify the ratio 12:18.

• Find the GCF of 12 and 18, which is 6.
• Divide both terms by 6:

  and .

• The simplified ratio is 2:3.

Tip: Always simplify ratios to their lowest terms.

4. Types of Ratios

a) Equivalent Ratios

• Ratios that represent the same relationship are called equivalent ratios.
• Equivalent ratios are obtained by multiplying or dividing both terms of a ratio by the same number.

Example: The ratios 2:3, 4:6, and 6:9 are equivalent because:

• Multiply 2:3 by 2: .
• Multiply 2:3 by 3: .

b) Comparing Ratios

To compare two or more ratios:

1. Convert them into fractions.
2. Find their equivalent forms so that the denominators are the same.
3. Compare the numerators to determine the larger or smaller ratio.

Example: Compare 3:4 and 5:6.

• Convert to fractions: and .
• Find the LCM of 4 and 6, which is 12.
• Convert to like fractions: and .
• Compare numerators: 9 < 10, so 3:4 < 5:6.

5. Proportion: Ratio and Proportion

• Proportion is a statement that two ratios are equal.
• If two ratios are equivalent, they are said to be in proportion.
• The symbol for proportion is :: (double colon).

Example: If 2:3 and 4:6 are equivalent, we write: .

Key Terms in Proportion:

1. Extremes: The first and last terms in a proportion.
2. Means: The middle two terms in a proportion.

In the proportion a:b :: c:d,

• a and d are the extremes.
• b and c are the means.

Property of Proportion: Ratio and Proportion

The product of the extremes is equal to the product of the means.

 

Example: Check if 2:3 and 4:6 are in proportion.

• Product of extremes: .
• Product of means: .
• Since both are equal, the ratios are in proportion.

6. Unitary Method: Ratio and Proportion

The unitary method is a technique used to solve problems involving ratios and proportions. It involves finding the value of a single unit and then using it to find the value of multiple units.

Steps in the Unitary Method:

1. Find the value of one unit.
2. Multiply the value of one unit by the required number of units.

Example: If the cost of 5 pens is Rs. 50, what is the cost of 8 pens?

• Cost of 1 pen = rupees.
• Cost of 8 pens = rupees.

7. Real-Life Applications of Ratio and Proportion:Ratio and Proportion

Ratios and proportions are used in various real-life situations, such as:

1. Cooking and Recipes: Measuring ingredients in the correct ratio.
2. Maps and Scale Drawings: Representing distances on maps.
3. Comparing Quantities: Comparing heights, weights, or prices.
4. Sharing and Distribution: Dividing amounts in a specific ratio.
5. Speed, Time, and Distance: Calculating travel times based on proportions.

Example: If a recipe requires 2 cups of flour and 1 cup of sugar, the ratio of flour to sugar is 2:1.

8. Solved Examples: Ratio and Proportion

Example 1: Simplify the ratio 15:25.

Solution:

• Find the GCF of 15 and 25, which is 5.
• Divide both terms by 5: , .
• The simplified ratio is 3:5.

Example 2: Check if 6:8 and 9:12 are in proportion.

Solution:

• Product of extremes: .
• Product of means: .
• Since both products are equal, the ratios are in proportion.

Example 3: Divide Rs. 1000 in the ratio 2:3.

Solution:

• Total parts = 2 + 3 = 5.
• Value of one part = .
• Share of the first part = .
• Share of the second part = .
• The amounts are Rs. 400 and Rs. 600.

9. Practice Questions

1. Simplify the following ratios: a) 18:24
   b) 35:50
2. Check if the following are in proportion: a) 4:6 and 8:12
   b) 5:10 and 15:30
3. Divide Rs. 600 in the ratio 3:2.
4. If 6 oranges cost Rs. 30, find the cost of 15 oranges.
5. A map has a scale of 1 cm : 10 km. If the distance between two cities is 5 cm on the map, what is the actual distance?

10. Summary

• A ratio compares two quantities of the same kind using division.
• Ratios are simplified to their lowest terms.
• Proportion is a statement that two ratios are equal.
• In a proportion, the product of the extremes equals the product of the means.
• The unitary method helps solve problems involving ratios and proportions.
• Ratios and proportions are widely used in real-life applications like cooking, map reading, and financial calculations.

Download PDF Notes and Excercise solution of the Chapter.

 

Chapter-9: Symmetry

Please Visit Readspot for Hindi Medium Study Material