Chapter 11: Algebra -Mathematics

ALGEBRA

Algebra is a branch of mathematics that can substitute letters for numbers to find the unknown. It can also be defined as putting real-life variables into equations and then solving them. The word Algebra is derived from Arabic “al-jabr”, which means the reunion of broken parts. Below are some algebra problems for students to practice.

Variable

A variable is an unknown quantity that is prone to change with the context of a situation.

Example: In the expression 2x + 5, x is the variable.

Constant

Constant is a quantity which has a fixed value. In the given example 2x + 5, 5 is the constant.

Terms of an Expression

Parts of an expression which are formed separately first and then added or subtracted, are known as terms.

In the above-given example, terms 2x and 5 are added to form the expression (2x + 5).

Factors of a term

Parts of an expression which are formed separately first and then added or subtracted, are known as terms.

Factors of a term are quantities which cannot be further factorized.

In the above-given example, factors of the term 2x are 2 and x.

Coefficient of a term

The numerical factor of a term is called the coefficient of the term.

In the above-given example, 2 is the coefficient of the term 2x.

To know more about Term, factor and Coefficient,

Like and Unlike Terms

Like terms

Terms having the same variables are called like terms.>

Example: 8xy and 3xy are like terms.

Unlike terms

Terms having different variables are called, unlike terms.

Example: 7xy and -3x are unlike terms.

To know more about “Algebra Basics”,

Monomial, Binomial, Trinomial and Polynomial Terms

Name	Monomial	Binomial	Trinomial	Polynomial
No. of terms	1	2	3	>3
Example	7xy	(4x−3)	(3x+5y−6)	(6x+5yx−3y+4)

 

Formation of Algebraic Expressions

Combinations of variables, constants and operators constitute an algebraic expression.

Example: 2x + 3, 3y + 4xy, etc.

To know more about Algebraic Expressions,

Addition and Subtraction of Algebraic Expressions

Addition and Subtraction of like terms

Sum of two or more like terms is a like term.

Its numerical coefficient will be equal to the sum of the numerical coefficients of all the like terms.

Example:  8y + 7y =?

Difference between two like terms is a like term.

Its numerical coefficient will be equal to the difference between the numerical coefficients of the two like terms.

Example: 11z − 8z =?

Addition and Subtraction of unlike terms

For adding or subtracting two or more algebraic expressions, like terms of both the expressions are grouped together and unlike terms are retained as it is.

Addition of −5x2 + 12xy and 7x2 + xy + 7x is shown below:

Subtraction of −5x2 + 12xy and 7x2 + xy + 7x is shown below:

Algebra as Patterns

To understand the relationship between patterns and algebra, we need to try making some patterns. We can use pencils to construct a simple pattern and understand how to create a general expression to describe the entire pattern. It would be best if you had a lot of pencils for this. It will help if they are of similar height.

Find a solid surface and arrange two pencils parallel to each other with some space in between them. Add a second layer on top of it and another on top of that, as shown in the image given below.

There are a total of six pencils in this arrangement. The above arrangement contains three layers, and each layer has a fixed count of two pencils. The number of pencils in each layer never varies, but the number of layers you wish to build is entirely up to you.

Current Number of Layers = 4

Number of Pencils per Layer = 2

Total Number of Pencils = 2 × 4 = 8

What if you increase the number of layers to 10? What if you keep building up to a layer of 100? Can you sit and stack those many layers? Here, the answer is obviously NO. Instead, let’s try to calculate.

Number of Layers = 100

Number of Pencils per Layer = 2

Total Number of Pencils = 2 × 100 = 200

There is an obvious pattern here. A single level has 2 pencils, which is always constant, regardless of the number of levels built. So to get the total number of pencils, we have to multiply 2 (the number of pencils per level) with the number of levels built. For example, to construct 30 levels, you will need 2 multiplied 30 times which is 60 pencils.

According to the previous calculation, to make a building of ‘x’ number of levels, we will require 2 multiplied ‘x’ times, and thus the number of pencils equal to 2x. We just created algebraic expressions based on patterns. In this way, we can make several algebra patterns.

Algebra as generalized Arithmetic Patterns

There are different types of algebraic patterns such as repeating patterns, growth patterns, number patterns, etc. All these patterns can be defined using different techniques. Let’s go through the algebra patterns using matchsticks given below.

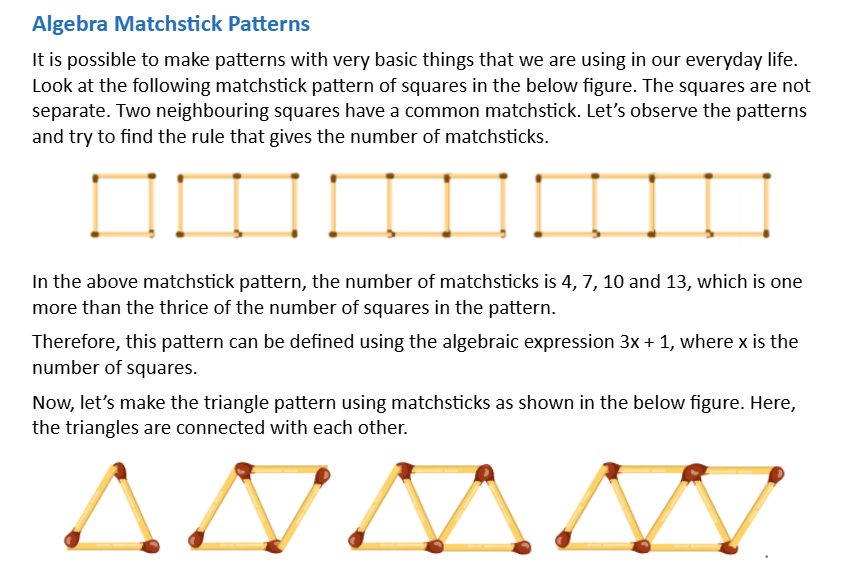
Number patterns

If a natural number is denoted by n, then its successor is (n + 1).

Example: Successor of n = 10 is n + 1 = 11.

If a natural number is denoted by n, then 2n is an even number and (2n + 1) is an odd number.

Example: If n = 10, then 2n = 20 is an even number and 2n+1=21 is an odd number.

Number Pattern Example

Consider an example given here. The given sequence of numbers is 11, 17, 23, 29, 35, 41, 47, and 53. The following figure helps to understand the relationship between the numbers.

In the given pattern, the sequence is increased by 6. It means the addition of the number 6 to the previous number gives the succeeding number. Also, the difference between the two consecutive number is 6.

Number Patterns Using Dots

Let’s start representing each whole number with a set of dots and arranging these dots in some elementary shape to find number patterns. For arranging these dots, we take strictly four shapes into account. Numbers can be arranged into:

• A line
• A rectangle
• A square
• A triangle

Line

Every number can be arranged in a line. Examples:

The number 2 can be represented by

The number 3 can be represented by

All other numbers can be represented in a similar pattern.

Rectangle

Some numbers can be arranged as a rectangle. Examples:

The number 6 can be arranged as a rectangle with 2 rows and 3 columns as

Similarly, 12 can be arranged as a rectangle with 3 rows and 4 columns as

Or as a rectangle with 2 rows and 6 columns as

Similar it can be formed by 8, 10, 14, 15, etc.

Square

Some numbers can be arranged as squares. Examples:

The number 4 can be represented as and 9 as

Similar it can be formed by 16, 25, 36, 49 and so on.

Triangle

Some numbers can be arranged as triangles. Examples:

The number 3 can be represented as and 6 as

Similar it can be formed by 10, 15, 21, 28, etc. It is to be noted that the triangle should have its 2 sides equal. Hence, the number of dots in the rows starting from the bottom row should be like 4,3,2,1. The top row should always have one dot.

Number Pattern Types

There are different types of number patterns in Mathematics. They are:

• • Arithmetic Sequence
  • Geometric Sequence
  • Square Numbers
  • Cube Numbers
  • Triangular Numbers
  • Fibonacci Numbers

• Number Patterns Observation

Observation of number patterns can guide to simple processes and make the calculations easier.

Consider the following examples which help the addition and subtraction with numbers like 9, 99, 999, etc. simpler.

145 + 9 = 145 + 10 – 1 = 155 – 1 = 154

145 – 9 = 145 – 10 + 1 = 135 + 1 =  136

145 + 99 = 145 + 100 – 1 = 245 – 1 = 244

145 – 99 = 145 – 100 + 1 = 45 + 1 = 46

Consider another pattern which simplifies multiplication with 9, 99, 999, and so on:

62 x 9 = 62 x (10 – 1) = 558

62 x 99 = 62 x (100 – 1) = 6138

62 x 999 = 62 x (1000-1) = 61938

Consider the following pattern which simplifies multiplication with numbers like 5, 25, 15, etc.:

48 x 5 = 48 x 10/2 = 480/2 = 240

48 x 25 = 48 x 100/4 = 4800/4 = 1200

48 x 125 = 48 x 1000/8 = 48000/8 = 6000

A number of patterns of similar fashion can be observed in the whole numbers which simplifies calculations to quite an extent.

To learn more about the number patterns in whole numbers, download BYJU’S – The Learning App. Subscribe to our YouTube channel to watch interesting videos on numbers.

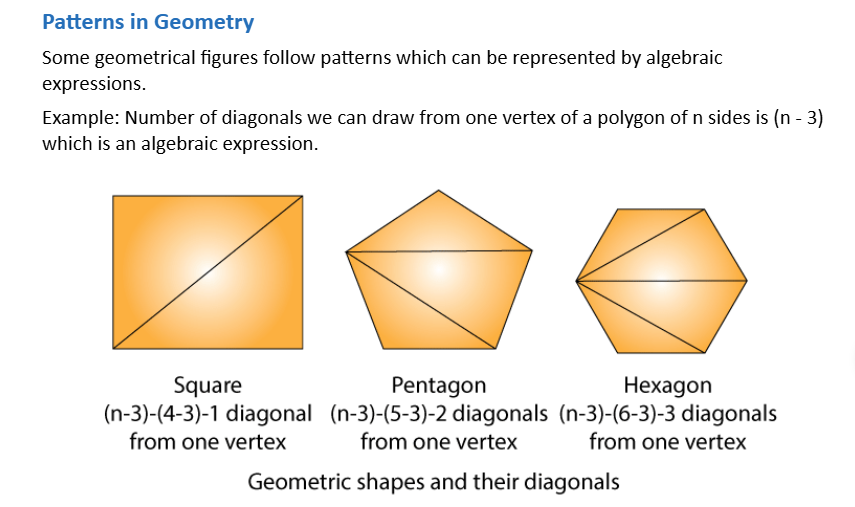
Algebraic expressions in perimeter and area formulae

Algebraic expressions can be used in formulating perimeter of figures.

Example: Let L be the length of one side then, the perimeter of:

An equilateral triangle = 3L.

A square = 4L.

A regular pentagon = 5L.

Algebraic expressions can be used in formulating area of figures.

Example: Area of:

Square = l2 where l is the side length of the square.

Rectangle = l × b, where l and b are lengths and breadth of the rectangle.

Triangle = 1/2 b × h where b and h are base and height of the triangle.

Equation

An equation is a condition on a variable which is satisfied only for a definite value of the variable.

The left-hand side (LHS) and right-hand side (RHS) of an equation are separated by an equality sign. Hence LHS = RHS.

If LHS is not equal to RHS, then it is not an equation.

Solving an Equation

Value of a variable in an equation which satisfies the equation is called its solution.

One of the simplest methods of finding the solution of an equation is the trial-and-error method.

 

Important Questions of  Algebra

 

Multiple Choice Questions:

Question 1. The rule, which gives the number of matchsticks required to make the matchstick pattern L, is

(a) 2 n

(b) 3 n

(c) 4n

(d) 5 n.

Question 2. The rule, which gives the number of matchsticks required to make the matchstick pattern C, is:

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n.

Question 3. The rule, which gives the number of matchsticks required to make the matchstick pattern F, is:

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n.

Question 4. The rule, which gives the number of matchsticks required to make the matchstick pattern U, is

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n.

Question 5. The rule, which gives the number of matchsticks required to make the matchstick pattern V, is:

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n.

Question 6. The rule, which gives the number of matchsticks required to make the matchstick pattern A, is:

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n.

Question 7. The rule, which gives the number of matchsticks required to make the matchstick pattern [], is

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n

Question 8. The rule, which gives the number of matchsticks required to make the matchstick pattern ≅, is:

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5 n.

Question 9. The rule, which gives the number of matchsticks required to make the matchstick pattern E. is:

(a) 2 n

(b) 3 n

(c) 4 n

(d) 5n.

Question 10. The rule, which gives the number of matchsticks required to make the matchstick pattern A, is:

(a) 3 n

(b) An

(c) 5 n

(d) 6 n.

Question 11. The rule, which gives the number of matchsticks required to make the matchstick pattern A, is

(a) 3 n

(b) 4 n

(c) 5 n

(d) 6 n.

 

Question 12. The rule, which gives the number of matchsticks required to make the matchstick pattern S, is:

(a) 3 l

(b) 4 n

(c) 5 n

(d) 6 n.

Question 13. The side of a square is l. Its perimeter is:

(a) 3l

(b) 2l

(c) 4l

(d) 6l

Question 14. 14. The side of an equilateral triangle is l. Its perimeter is:

(a) l

(b) 2l

(c) 3l

(d) 6l.

Question 15. The side of a regular pentagon is l. Its perimeter is:

(a) 3l

(b) 6l

(c) 4l

(d) 5l

 

Match The Following:

	Column I		Column II
1.	3 times y added to 13	A.	5y – 8
2.	8 subtracted from 5 times y	B.	3x – 5
3.	5 reduced from 3 times x	C.	2x + 5
4.	5 added to double of x	D.	3y + 13

Fill in the blanks:

1. The value of 2x – 12 is zero, when x = ________.
2. The product of 2 and x is being added to the product of 3 and y is expressed as ________.
3. The numerical coefficient of the terms 12xy2+12xy2 is ________.
4. The no. of terms in the expression 3x2y-4x2y2+12xy2-5x is ________.

True /False:

1. The parts of an algebraic exponent which are connected by + or – sign are called its terms.
2. 5 times x subtracted from 8 times y is 5x – 8y.
3. A number having fixed value is called variable.
4. The numerical coefficient of -2x2y is -2.

Very Short Questions:

1. Write which letters give us the same rule as that given by L.
2. Rearrange the terms of the following expressions in ascending order of powers of x:

5x2, 2x, 4x4, 3x3, 7x5

1. Give expressions for the following

1. 7 added to
2. 7 subtracted from
3. p multiplied by
4. p divided by
5. 7 subtracted
6. -p multiplied by
7. -p divided by
8. p multiplied by – 5.

1. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students ? (Use s for number of students.)
2. Form expressions using y, 2 and 7. Every expression must have y in it. use only two number operations. These should be different.
3. Find the value of the expression 2x – 3y + 4z, if x = 10, y = -12 and z = 11.
4. Six less than a number equals to two. What is the number?
5. Write an algebraic expression for each of the following:

(a) 3 subtracted from a number y.

(b) 5 is added to three times a number x.

1. Write an algebraic expression for the following expressions:

(a) The sum of a number x and 4 is doubled.

(b) One fourth of a number x is added to one third of the same number.

Short Questions:

1. Think of a number x. Multiply it by 3 and add 5 to the product and subtract y subsequently. Find the resulting number.
2. Here is a pattern of houses with matchsticks:

Write the general rule for this pattern.

1. If the side of an equilateral triangle is x, find its perimeter.
2. If x = 3, find the value of the following:

(i) x + 5

(ii) 2x – 3

(iii) x – 7

(iv) x3 – 1

1. If x = 2, y = 3 and 2 = 5, find the value of;

(a) 2x + y + z

(b) 4x -y + z

(c) x – y + z

1. State which of the following are equations with a variable?

(a) 12 = x – 5

(b) 2x > 7

(c) x2 = 5

(d) 5 + 7 = 3 + 9

(e) 7 = (11 × 5) – (12 × 4)

1. Think of a number, add 2 to it and then multiply the sum by 6, the result is 42.
2. The side of a regular hexagon is s cm. Find its perimeter.
3. If a = 3, b = 12 and c = 14 , find the value of

1. Complete the table and find the solution of the equation 19 – x = 13

 

Long Questions:

1. If x = –12, y = 14 and z = 0, find the value of the given expressions

(a) 8z + 2x -y

(b) z – y + 3x

1. A starts his car from Delhi at 6.00 am to Amritsar. The uniform speed of his car is x km/h. At 12.00 noon, he finds that he is still 50 km away from Amritsar. Find the distance between Delhi and Amritsar.
2. Anshika’s Score in Science is 15 more than the two-third of her score in Sanskrit. If she scores x marks in Sanskrit, find her score in Science.
3. Deepak’s present age is one-third his mother’s present age. If the mother’s age was five times his age 6 years ago, what are their present ages?

Assertion and Reason Questions:

1.) Assertion (A) – The rule, which gives the number of matchsticks required to make the matchstick pattern L, is 2n.

Reason (R) – For n = 1, the number of matchsticks required = 2 × 1 = 2

1. a) Both A and R are true and R is the correct explanation of A
2. b) Both A and R are true but R is not the correct explanation of A
3. c) A is true but R is false
4. d) A is false but R is true

2.) Assertion (A) – The rule, which gives the number of matchsticks required to make the matchstick pattern C, is3n

Reason (R) – For n = 2, the number of matchsticks required = 2 × 2 = 4

1. a) Both A and R are true and R is the correct explanation of A
2. b) Both A and R are true but R is not the correct explanation of A
3. c) A is true but R is false
4. d) A is false but R is true

ANSWER KEY –

Multiple Choice questions:

• (a) 2 n

1.  (b) 3 n
2.  (c) 4 n
3.  (b) 3 n
4.  (a) 2 n
5.  (b) 3 n
6.  (c) 4 n
7.  (a) 2 n
8.  (d) 5n
9.  (c) 5 n
10.  (a) 3 n
11.  (c) 5 n
12.  (c) 4l
13.  (c) 3l
14.  (d) 5l

Match The Following:

	Column I		Column II
1.	3 times y added to 13	D.	3y + 13
2.	8 subtracted from 5 times y	A.	5y – 8
3.	5 reduced from 3 times x	B.	3x – 5
4.	5 added to double of x	C.	2x + 5

 

Fill in the blanks:

1. The value of 2x – 12 is zero, when x = 6.
2. The product of 2 and x is being added to the product of 3 and y is expressed as 2x + 3y.
3. The numerical coefficient of the terms 12xy2+12xy2 is 12.
4. The no. of terms in the expression 3x2y-4x2y2+12xy2-5x is 4.

True /False:

1. True
2. False
3. False
4. True

Very Short Answer:

1. The other letters which give us the same rule as L are T, V and X because the number of matchsticks required to make each of them is 2.
2. If the given terms are arranged in the ascending order of powers of x, we get,2x, 5x2, 3x3, 4x4, 7x5.
3. (i) p + 7

(ii) p – 7

(iii) 7p

(iv) p7

 (v) – m – 7

(vi) -5p

(vii) −p5

(viii) – 5p.

1. Number of pencils to be distributed to each student= 5And, let the number of students in class be ‘s’. As per the logic, Number of pencils needed =(Number of students in the class) x. (Number of pencils to be distributed to one student )

So, Number of pencils needed = 5 x s = 5s.

1. The different expressions that can formed are: 2y + 7, 2y – 7, 7y + 2, 7y-2, (y/2) – 7, (y/7)-2, y – (7/2), y + (7/2)
2. Given expression = 2x – 3y + 4z

If x = 10, y = -12 and z = 11,

The expression becomes, (2 × 10) (3 × -12) + (4 × 11)

= 20 – (-36) + 44

= 20 + 36 + 44

= 100.

1. Let the number be ‘x’.

According to condition, we have x – 6 = 2

By inspections, we have 8 – 6 = 2

∴ x = 8

Thus, the required number is 8.

1. (a) The required expression is y – 3

(b) The required expression is 5 + 3x

1. (a) The required expression is 2 x (x + 4)

(b) The required expression is 14x +13x

Short Answer:

1. Required number is (3x + 5)

Now we have to subtract y from the result i.e., 3x + 5 – y

1. One house is made of 6 matchsticks i.e. 6 × 1

Two houses are made of 12 matchsticks i.e. 6 × 2

Three houses are made of 18 matchsticks i.e. 6 × 3

∴ Rule is 6n where n represents the number of houses.

1. We know that the three sides of an equilateral triangle are equal.

∴ x + x + x = 3x.

Thus, the required perimeter = 3x units.

1. Given that x = 3

(i)x + 5 = 3 + 5 = 8

(ii) 2x – 3 = 2 x 3 – 3 = 6 – 3 = 3

(iii) x – 7 = 3- 7 = -4

(iv) x3– 1 =33 -1 = 1 – 1 = 0

1. (a) Given that: x – 2, y = 3 and z = 5

∴ 2x + y + 2 = 2 x 2 + 3 + 5

= 4 + 3 + 5 = 12

(b) 4x – y + z = 4 x 2 – 3 + 5

= 8 – 3 + 5 = 5 + 5 = 10

(c) x – y + z = 2 – 3 + 5 = -1 + 5 = 4

1. (a) 12 = x – 5 is an equation with a variable x.

(b) 2x > 7 is not an equation because it does not have ‘=’ sign.

(c) x2 = 5 is an equation with a variable x.

(d) 5 + 7 = 3 + 9 is not an equation because it has no variable.

(e) 7 = (11 × 5) – (12 × 4) is not an equation because it has no variable.

1. Let the number be x.

∴ Sum of x and 2 = x + 2

Now by multiplying the sum by 6, we get

6 × (x + 2) = 42

⇒ 6 × x + 6 × 2 = 42

⇒ 6x + 12 = 42

By inspection, we get

6 × 5 + 12 = 42

⇒ 30 + 12 = 42

∴ 42 = 42

So, the required number = 5

1. Each side of a regular hexagon = s

∴ its perimeter = s + s + s + s + s + s = 6s cm

1. By inspection, we have

Thus, the required solution is 6.

Long Answer:

1. Time taken by A to reach Amritsar = 12.00 noon – 6.00 am = 6 hour.

The uniform speed of the car = x km/ hr

∴ Total distance covered by A = Time x speed = 6x km.

∴ Distance between Delhi and Amritsar = (6x + 50) km

1. Anshika’s score in Sanskrit = x

∴ Her marks in Science = 23x + 15

∴ Thus, Anshika’s score in Science = 23x + 15

1. Let present age of mother = x years

Deepak’s present age = x3 years

6 years ago, mother’s age = (x – 6) years

Deepak’s age = x3-6 years

According to the problem, 6 years ago, mother’s age is 5 times Deepak age.

Therefore, present age of mother = 36 years and

Assertion and Reason Answers:

1) a) Both A and R are true and R is the correct explanation of A

2) a) Both A and R are true and R is the correct explanation of A

 

Download PDF Notes and Excercise solution of the Chapter.

 

Chapter-12: Ratio and Proportion

 

Please Visit Readspot for Hindi Medium Study Material