Chapter 11: Mensuration
Chapter 11: Mensuration

Introduction to Mensuration
Mensuration is a fundamental branch of mathematics that focuses on the precise measurement of geometric shapes, including their lengths, areas, and volumes. Derived from the Latin word “mensura,” meaning “to measure,” it combines principles from geometry and algebra to calculate the perimeter (the boundary length of a two-dimensional figure), area (the space enclosed by a shape), and for three-dimensional solids, surface area (the total outer covering) and volume (the space occupied within). In Class 8, Chapter 11 of the NCERT Mathematics textbook introduces these concepts through practical examples, emphasizing their applications in everyday life, such as fencing a garden, calculating carpet area for a room, or determining the volume of a water tank.
The chapter begins by revisiting basic shapes like rectangles and squares, then progresses to more complex figures like trapeziums, general quadrilaterals, and polygons. It also extends to solids such as cuboids, cubes, and cylinders. Key to understanding mensuration is recognizing units: lengths in meters (m) or centimeters (cm), areas in square units (m² or cm²), and volumes in cubic units (m³ or cm³). Conversions are crucial—1 m² = 10,000 cm², and 1 m³ = 1,000 liters. The chapter uses π ≈ 22/7 or 3.14 for circular calculations and stresses deriving formulas logically rather than rote memorization.
Perimeter and Area of Plane Figures
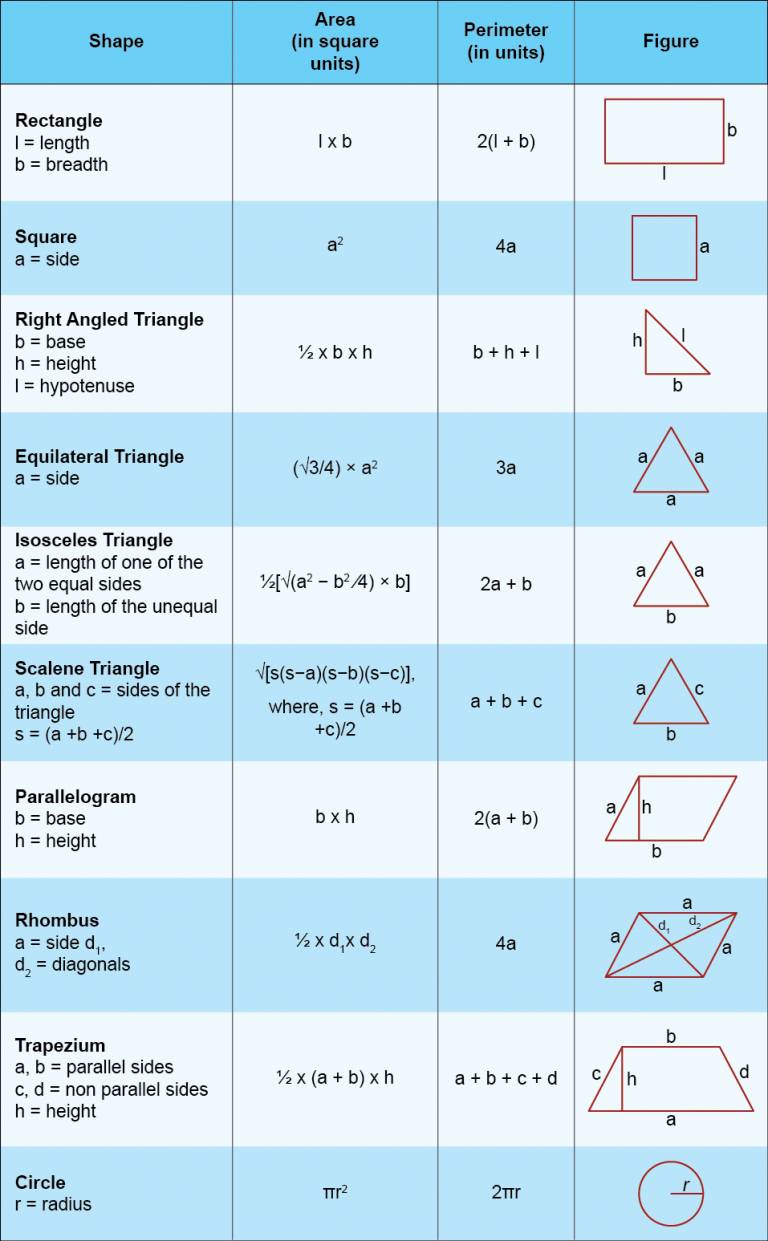
The chapter dedicates significant space to two-dimensional (plane) figures, starting with familiar shapes and building toward irregular ones. Perimeter is simply the sum of all side lengths, while area formulas often involve base, height, or diagonals.
For a rectangle, with length l and breadth b, the perimeter is 2(l + b), representing the fencing needed around a rectangular field. The area is l × b, useful for calculating floor covering. A square, a special rectangle where all sides equal s, has perimeter 4s and area s². These are revisited with problems like comparing a square and rectangular field of equal perimeter (e.g., if the rectangle is 50 m by 30 m, perimeter = 160 m, so square side = 40 m; area comparison shows square larger at 1,600 m² vs. 1,500 m²).
Triangles follow, with area = ½ × base × height, regardless of shape (equilateral, isosceles, or scalene). For an equilateral triangle with side a, area = (√3/4) a². Perimeter is the sum of sides a + b + c. Parallelograms, with opposite sides equal, have area = base × height and perimeter 2(l + b). A rhombus, a parallelogram with all sides equal, uses diagonals d₁ and d₂ for area = ½ × d₁ × d₂, as diagonals bisect each other at right angles.
Circles introduce curved boundaries: circumference (perimeter) = 2πr, and area = πr². The chapter illustrates with a circular park path, where the area between two concentric circles (annulus) is π(R² – r²).
A key section covers trapeziums, quadrilaterals with one pair of parallel sides (a and b). The area formula, ½ × (a + b) × h (height between parallels), is derived creatively: by dividing into a rectangle and two triangles, or by “flipping” one triangle to form a larger triangle of equal area. For example, if parallels are 10 m and 20 m, height 5 m, area = ½ × 30 × 5 = 75 m². This method highlights problem-solving without advanced tools.
General quadrilaterals (not necessarily parallelograms) require drawing a diagonal d to split into two triangles. If perpendicular heights from opposite vertices to the diagonal are h₁ and h₂, area = ½ × d × (h₁ + h₂). This applies to irregular shapes too.
Polygons, with n sides, are tackled by dividing into triangles or trapeziums. For a regular polygon, approximate area uses triangulation from the center, but the chapter focuses on irregular ones via decomposition. An example: a pentagon divided into three triangles and a rectangle yields combined areas.
These concepts are reinforced through exercises, like finding the cost of wiring a trapezoidal park or painting a polygonal wall, blending math with real-world budgeting (e.g., ₹5 per m²).
Surface Area and Volume of Three-Dimensional Solids
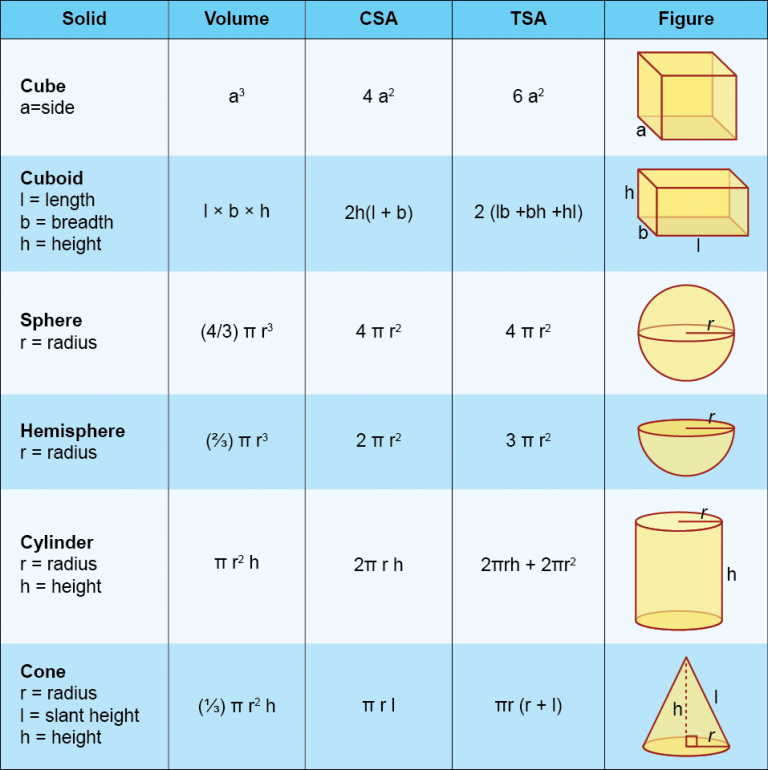
Shifting to solids, the chapter explores cuboids, cubes, and cylinders—shapes with length, breadth, height, or radius. Surface area includes total (all faces) and lateral (sides only), while volume measures internal space.
A cuboid has three dimensions: length l, breadth b, height h. Total surface area (TSA) = 2(lb + bh + hl), summing pairs of rectangular faces. Lateral surface area (LSA) = 2h(l + b), for the sides excluding top and bottom. Volume = l × b × h. Diagonal = √(l² + b² + h²*). Example: A room 5 m × 4 m × 3 m needs painting on four walls (LSA = 2×3×(5+4) = 54 m²) and ceiling (area 20 m²), total 74 m² at ₹10/m² costs ₹740.
A cube, with equal edges a, simplifies to TSA = 6a², LSA = 4a², volume = a³, diagonal = a√3. It’s like a cuboid with l = b = h.
Cylinders are prisms with circular bases. For radius r and height h, LSA (curved surface) = 2πrh*, TSA = 2πr(r + h) (adding two bases πr² each), volume = πr²h. A right circular cylinder has bases perpendicular to the axis. Example: A tin 10 cm high, 7 cm radius, holds volume π×49×10 ≈ 1,540 cm³ (1.54 L), useful for packaging.
The chapter distinguishes congruent faces (identical in shape/size) and notes capacity (e.g., 1 L = 1,000 cm³). Problems involve combining solids, like a cuboidal box with cylindrical holes, but focus on basics.
Applications and Exercises
Mensuration’s power lies in applications: agriculture (field areas), architecture (room volumes), manufacturing (material costs). Exercises include 25 questions, from simple (area of a 12 m × 8 m rectangle = 96 m²) to multi-step (trapezium with non-parallel sides 13 m, 14 m, parallels 10 m, 18 m; height via Pythagoras ≈ 12 m, area ≈ 168 m²).
In summary, Chapter 11 equips students with tools for quantitative reasoning, emphasizing derivation and visualization. Mastering these fosters problem-solving for higher classes, where irregular solids and calculus extend these ideas.
Some importent Solved Examples:
1. Calculate the area of a square with side 5 cm.
The area of a square of side 5cm is A=L^2=5^2=25 cm^2
2. Calculate the perimeter of a rectangle having a length of 10 cm and breadth of 5 cm.
The perimeter of a rectangle with length 10 cm and breadth 5 cm is 2( l + b) = 2(10 + 5) = 30 cm.
3. What is the area of a right-angled triangle with two of its perpendicular sides as 3 and 4 cm?
The area of a right angled triangle with two of its perpendicular sides as 3 cm and 4 cm is:
A = ½ x b x h = 0.5 x 3 x 4 = 6 cm2.
4. Calculate the volume of a cone having a radius of 7 cm and height of 5 cm?
The volume of a cone with a radius of 7 cm and height of 5 cm is:
(1/3)πr2h=256.67 cm3
5. What is the total surface area and curved surface area of a cylinder with a radius of 14 cm and height of 10 cm?
The total surface area of a cylinder with radius 14 cm and height 10 cm is:
2πrh+2πr2=2112 cm2
The curved surface area of a cylinder with radius 14cm and height 10cm is:
2πrh=880 cm2
Download pdf notes and Sulutions of the Chapter:
Please Visit Readspot for Hindi Medium Study Material
Importent Formula of this chapter..