Symmetry – Notes for CBSE Class 7 Maths

Introduction to Symmetry

Symmetry is a concept that we observe in everyday life—whether it’s in nature, art, or objects around us. In mathematics, symmetry refers to a property where one half of a figure is a mirror image of the other half. This chapter introduces students to the idea of symmetry, focusing on lines of symmetry and rotational symmetry, and how these apply to shapes and figures.

1. What is Symmetry?

• Symmetry means balance or similarity in shape, size, and position.
• A figure is said to be symmetrical if it can be divided into two identical parts that are mirror images of each other.
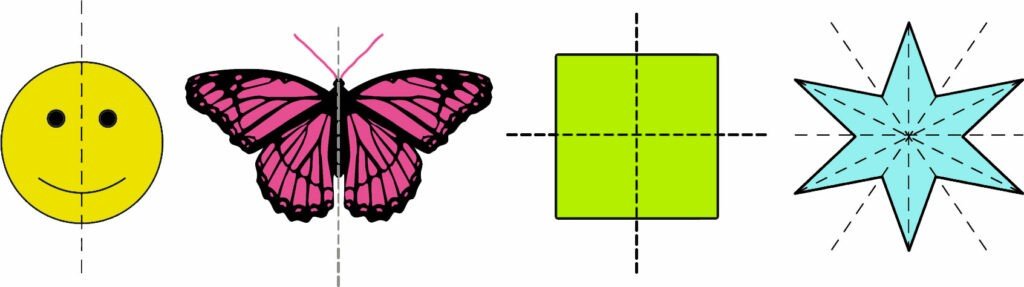
• Example: A butterfly has symmetry because its left and right wings are mirror images.

2. Line Symmetry (Reflection Symmetry)

• Definition: A figure has line symmetry if it can be folded along a line so that one half perfectly overlaps the other half. This line is called the line of symmetry (or axis of symmetry).
• The line of symmetry acts like a mirror.
• A figure can have one, multiple, or no lines of symmetry.

Examples of Line Symmetry:

1. Square: A square has 4 lines of symmetry.
   • Two diagonals.
   • Two lines passing through the midpoints of opposite sides (vertical and horizontal).
2. Rectangle: A rectangle has 2 lines of symmetry.
   • One vertical line through the center.
   • One horizontal line through the center.
3. Circle: A circle has infinite lines of symmetry (any line passing through the center).
4. Equilateral Triangle: It has 3 lines of symmetry (one from each vertex to the midpoint of the opposite side).
5. Isosceles Triangle: It has 1 line of symmetry (from the vertex between equal sides to the midpoint of the base).
6. Scalene Triangle: No lines of symmetry.

Key Points:

• Regular polygons (shapes with all sides and angles equal) have as many lines of symmetry as their number of sides. For example:
  • Pentagon (5 sides) → 5 lines of symmetry.
  • Hexagon (6 sides) → 6 lines of symmetry.
• Irregular shapes may have no symmetry.

3. How to Find the Line of Symmetry?

• Draw the shape on paper.
• Fold it along a line to see if the two halves match perfectly.
• If they do, that line is a line of symmetry.
• Alternatively, use a mirror to check if one half reflects the other.

4. Rotational Symmetry

• Definition: A figure has rotational symmetry if it looks the same after being rotated around a central point by a certain angle (less than a full turn of 360°).
• The point around which the figure is rotated is called the center of rotation.
• The smallest angle by which the figure can be rotated to look the same is called the angle of rotation.
• The number of times a shape fits onto itself in one full turn (360°) is called the order of rotational symmetry.

Examples of Rotational Symmetry:

1. Square:
   • Rotate it by 90°, 180°, 270°, or 360°, and it looks the same.
   • Order of rotational symmetry = 4 (fits 4 times in 360°).
   • Angle of rotation = 360° ÷ 4 = 90°.
2. Equilateral Triangle:
   • Rotate it by 120°, 240°, or 360°.
   • Order of rotational symmetry = 3.
   • Angle of rotation = 360° ÷ 3 = 120°.
3. Circle:
   • Looks the same after any rotation.
   • Infinite order of rotational symmetry.
4. Rectangle:
   • Rotate it by 180° or 360°.
   • Order of rotational symmetry = 2.
   • Angle of rotation = 360° ÷ 2 = 180°.

Key Points:

• A shape with no rotational symmetry (other than a full 360° turn) has an order of 1 (e.g., a scalene triangle).
• The center of rotation is usually the center of the shape.

5. Difference Between Line Symmetry and Rotational Symmetry

• Line Symmetry: Involves folding along a line to match two halves.
• Rotational Symmetry: Involves turning the shape around a point to look the same.
• Some shapes have both (e.g., square), some have only one (e.g., a parallelogram has rotational symmetry of order 2 but no line symmetry), and some have neither (e.g., a scalene triangle).

6. Symmetry in Letters and Words

• Symmetry can also be observed in the English alphabet and words.
• Letters with Line Symmetry:
  • Vertical symmetry: A, H, I, M, O, T, U, V, W, X, Y.
  • Horizontal symmetry: B, C, D, E, H, I, K, O, X.
• Letters with Rotational Symmetry:
  • N, S, Z (look the same after a 180° rotation).
• Words with Symmetry:
  • Example: “MOM” has vertical line symmetry.
  • Example: “NOON” has rotational symmetry (order 2).

7. Symmetry in Real Life

• Nature: Leaves, flowers (e.g., sunflower), and animals (e.g., starfish) show symmetry.
• Architecture: Buildings like the Taj Mahal have line symmetry.
• Art: Designs like rangoli often use both line and rotational symmetry.

8. Important Terms

• Line of Symmetry: The imaginary line dividing a figure into two mirror-image halves.
• Center of Rotation: The point around which a figure is rotated.
• Order of Rotational Symmetry: The number of times a shape matches itself in one full turn.
• Angle of Rotation: The smallest angle needed for the shape to look the same.

9. Practice Questions

1. How many lines of symmetry does a regular hexagon have?
   • Answer: 6
2. What is the order of rotational symmetry of a square?
   • Answer: 4
3. Does a parallelogram have line symmetry? Why or why not?
   • Answer: No, because it cannot be folded to match two halves perfectly.
4. Find the angle of rotation for an equilateral triangle.
   • Answer: 120°
5. Name a letter with both vertical and horizontal symmetry.
   • Answer: H, I, O, X

10. Activities to Understand Symmetry

• Paper Folding: Take a square paper, fold it along different lines, and check how many ways it matches perfectly.
• Drawing: Draw a shape (e.g., a star) and find its lines of symmetry using a ruler.
• Rotation Game: Trace a shape, rotate it around its center, and count how many times it looks the same in one full turn.

11. Summary

• Symmetry is about balance and repetition in shapes.
• Line symmetry involves a mirror-like division, while rotational symmetry involves turning a shape.
• Regular polygons have equal lines of symmetry and order of rotational symmetry.
• Symmetry is not just a math concept—it’s all around us in nature, art, and design.

---

Additional Notes for Better Understanding

• Visualizing Symmetry: Use a mirror or tracing paper to confirm lines of symmetry in complex shapes.
• Common Mistakes:
  • Confusing line symmetry with rotational symmetry.
  • Assuming all shapes have symmetry (e.g., a trapezium usually has no symmetry unless specified).
• Tips for Exams:
  • Memorize the number of lines of symmetry for basic shapes (square, rectangle, triangle, circle).
  • Practice identifying the order of rotational symmetry by mentally rotating shapes.

These notes cover all the essential topics in Chapter 14: Symmetry for CBSE Class 7 Maths. By understanding the concepts of line symmetry and rotational symmetry, along with practicing examples, students can master this chapter effectively.

Chapter 14 Symmetry