Chapter 8: Decimals- Mathematics

DECIMALS

The numbers used to represent numbers smaller than unit 1 are called decimal numbers. The decimal point or the period plays a significant part in a Decimal Number. This period separates the fractional part and whole number part in a decimal number. Place value of a digit can be defined as the value of a digit as per the place of that digit in a number.

Decimals Examples

Let us consider a decimal number 0.5694 to see the different place values of each digit:

• The value of the digit at the first place after the decimal point is tenths place value. Tenths can be calculated as 1 unit divided in 10 equal parts i.e. 0.1. Therefore, considering this there are 5 tenths in the number 0.5694.
• The value of the digit at the second place after the decimal point is hundredths place value. The number in that place tells you how many hundredths are there. Hundredths can be calculated as 1 unit divided in100 equal parts i.e. 0.01. Therefore, considering this there are 6 hundredths in the number 0.5694
• The value of the digit at the third place after the decimal point is thousandths place value. The number in that place tells you how many thousandths are present. Thousandths can be calculated as 1 unit divided in1000 equal parts i.e. 0.001. Therefore, considering this there are 9 thousandths in the number 0.5694
• Ten-thousandths
• The value of the digit at the fourth place after the decimal point is ten-thousandths place value. The number in that place tells you how many ten-thousandths are present. Ten-thousandths can be calculated as 1 unit divided into 10000 equal parts i.e. 0.0001. Therefore, considering this there are 4 thousandths in the number 0.5694

Introduction to decimals

• Decimals are used in many ways in our lives.
• For example, in representing units of money, length and weight.
• Example: Price of the book is Rs. 34.5

In Algebra, decimals are one of the types of numbers, which has a whole number and the fractional part separated by a decimal point. The dot present between the whole number and fractions part is called the decimal point. For example, 34.5 is a decimal number.

Here, 34 is a whole number part and 5 is the fractional part.

“.” is the decimal point. 

Let us discuss some other examples.

Here is the number “thirty-four and seven-tenths” written as a decimal number:

 

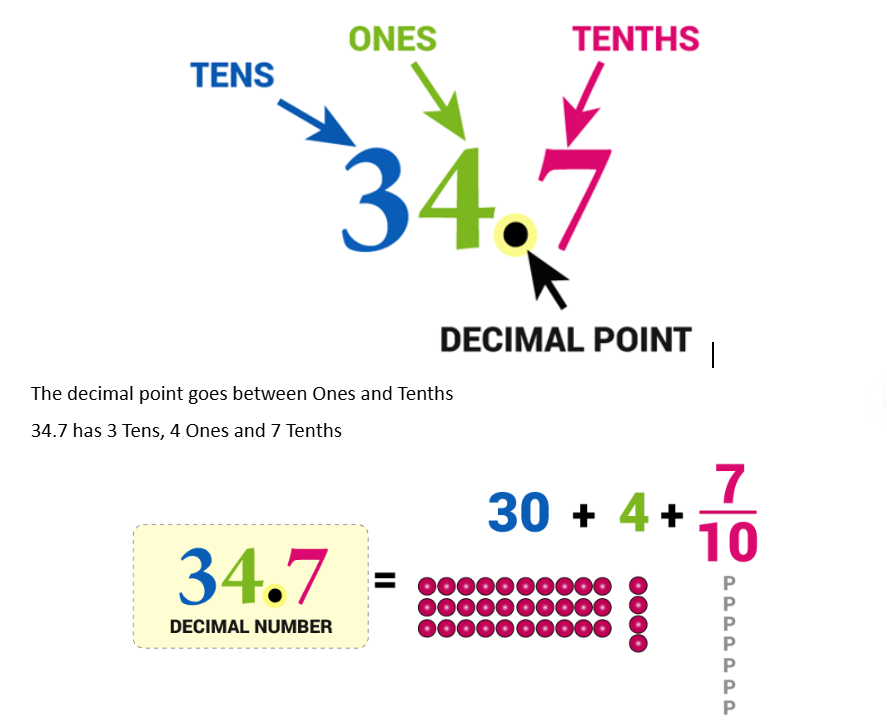
Types of Decimal Numbers

Decimal Numbers may be of different kinds, namely

Recurring Decimal Numbers (Repeating or Non-Terminating Decimals)

Example-

3.125125 (Finite)

3.121212121212….. (Infinite)

Non-Recurring Decimal Numbers (Non-Repeating or Terminating Decimals):

Decimal Fraction

It represents the fraction whose denominator in powers of ten.

Example:

81.75 = 8175/100

32.425 = 32425/1000

Converting the Decimal Number into Decimal Fraction:

For the decimal point place “1” in the denominator and remove the decimal point.

“1” is followed by a number of zeros equal to the number of digits following the decimal point.

For Example:

81.75 = 8175/100

8 represents the power of 101 that is the tenths position.

1 represents the power of 100 that is the units position.

7 represents the power of 10-1 that is the one-tenths position.

5 represents the power of 10-2 that is the one-hundredths position.

So that is how each digit is represented by a particular power of 10 in the decimal number.

Place Value in Decimals

The place value system is used to define the position of a digit in a number which helps to determine its value. When we write specific numbers, the position of each digit is important.

Example:

For instance, let’s consider the number 456.

• The position of “6” is in One’s place, which means 6 ones (i.e. 6).
• The position of “5” is in the Ten’s place, which means 5 tens (i.e. fifty).
• The position of “4” is in the Hundred’s place, which means 4 hundred.
• As we go left, each position becomes ten times greater.

Hence, we read it as “Four hundred fifty-six”.

As we move left, each position is 10 times bigger!

Tens are 10 times bigger than Ones.

Hundreds are 10 times bigger than Tens.

And

Each time we move right every position becomes 10 times smaller from Hundred’s to Ten’s, to Ones

But if we continue past Ones?

What are 10 times smaller than Ones?

Before that, we should first put a decimal point,

So we already know that where we put that decimal point.

We say the above example as four hundred and fifty-six and eight-tenths but we usually just say four hundred and fifty-six point eight.

The power of 10 can be found using the following Place Value Chart:

The digits to the left of the decimal point are multiplied with the positive powers of ten in increasing order from right to left.

The digits to the right of the decimal point are multiplied with the negative powers of 10 in increasing order from left to right.

Following the same example 81.75

The decimal expansion of this is:

{(8 × 10) + (1 × 1)} + {(7 × 0.1) + (5 × 0.01)}

Where each number is multiplied by its associated power of ten.

Properties of Decimals

The important properties of decimal numbers under multiplication and division operations are as follows:

 

• If any two decimal numbers are multiplied in any order, the product remains the same.
• If a whole number and a decimal number are multiplied in any order, the product remains the same.
• If a decimal fraction is multiplied by 1, the product is the decimal fraction itself.
• If a decimal fraction is multiplied by 0, the product is zero (0).
• If a decimal number is divided by 1, the quotient is the decimal number.
• If a decimal number is divided by the same number, the quotient is 1. 
• If 0 is divided by any decimal, the quotient is 0. 
• The division of a decimal number by 0 is not possible, as the reciprocal of 0 does not exist.

Example:

3.2376 (Finite)

3.137654….(Infinite)

Representing decimals on a number line

Example: Represent 1.3 on the number line.

1.3 is more than 1 but less than 2.

Divide each unit length into 10 equal parts. From 1, take 3 parts to the right and we will get 1.3.

A Little Secret About Fractions and Decimals

Inter-conversion of fractions and decimals

Fractions as decimals

12/5 = 24/10 = (20+4) / 10 = 20/10 + 4/10 = 2+0.4 = 2.4

Decimals as fractions

21.2 = 21 + (2/10) = (210/10) + (2/10) = (212/10) = (106/5)

Recurring and terminating decimals

A terminating decimal is a decimal number which has finite number of digits after the decimal.

Example: 0.35

A recurring decimal is one where its decimal representation becomes periodic or same sequence of digits keeps repeating indefinitely.

Example: 31.213333…

Decimal 1 vs. Decimal 2

Comparing decimals

Any two decimal numbers can be compared by comparing their whole part and decimal parts.

If the whole parts are equal then the tenth parts can be compared and so on.

Comparison when whole parts equal

Compare 22.3 and 22.5

Whole parts are equal. Hence we compare tenths part.

22.3=22 + 3/10

22.5 = 22 + 5/10

3/10<5/10

∴ 22.3 < 22.5.

Comparison whole parts are unequal

Tenths and Hundredths

191.8 = 191 + (8/10)

⇒ 8 occupies the tenths position.

Move the tenths place to the right by one unit, the place value decreases further to 1/100th (hundredth) place.

191.86 = 191 + 8/10 + 6/100

⇒ 6 occupies the hundredths place

Place values

Place value gives a value of the number depending on its location.

Place value table of 5.2 is as shown below.

Many Many Many Points Together

Addition of Decimals

Addition of 1.29 and 0.34

Thus, 1.29 + 0.34 = 1.63

Subtraction of Decimals

Subtraction of 5.25 from 8.28

Thus, 8.28 – 5.25 = 3.03

Multiplication of Decimals

Multiplication of 2.8 and 7

2.8 × 7 (There is only one digit to the right of the decimal point in 2.8)

28 × 7 (Ignoring the decimals)

28 × 7 = 196

Now bring the decimal back after one digit from left and thus answer is 19.6

Division of Decimals

Divide 3.4 by 2

3.4/2 = Quotient

Ignore the decimal and divide the numerator by the denominator. Here, quotient = 34/2 = 17

Since there is only one digit to the right of the decimal, put the decimal after one digit from left in the quotient. Therefore, quotient becomes 1.7

Points on How to Use the Points

Point shift trick

Division: Point is shifted to the left by the number of zeroes in the denominator.

150/100=1.50 (Shifting decimal by 2 points to the left)

1.5/1000=0.0015 (Shifting decimal by 3 points to the left)

Decimals in length measurement

1m = 100cm

1cm = 1/100m = 0.01m (Move decimal to left by 2 units in the numerator as there are two zeroes in the denominator)

150cm = 150/100m = 1.5m

Decimals in weight measurement

1 kg = 1000 g

1 g = 1/1000 kg

298 g = 298/1000 kg = 0.298 kg (Move the decimal to the left by 3 places in the numerator as there are 3 zeroes in the denominator)

 

Download PDF Notes and Excercise solution of the Chapter.

 

Chapter 9: Data Handling (Best Solution )