Exponents and Powers – Notes for CBSE Class 7 Maths

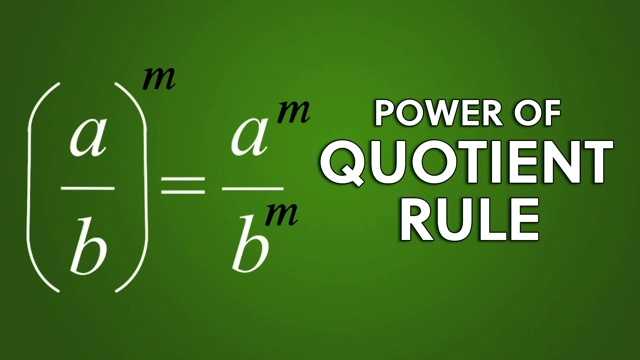
Introduction

Exponents and Powers are a way to represent repeated multiplication of a number by itself. This chapter introduces students to the concept of exponents, their rules, and their applications in simplifying large numbers. For example, instead of writing 2 × 2 × 2 × 2, we can write it as 2⁴, where 2 is the base and 4 is the exponent or power.

• Base: The number that is multiplied repeatedly.
• Exponent: The number of times the base is multiplied by itself.
• Example: In 5³, 5 is the base, and 3 is the exponent. It means 5 × 5 × 5 = 125.

The chapter emphasizes how exponents make calculations easier and are widely used in science, technology, and mathematics to express very large or very small numbers.

---

1. Expressing Numbers Using Exponents

Numbers can be written in exponential form to simplify them. For instance:Exponents and Powers

• 16 = 2 × 2 × 2 × 2 = 2⁴
• 27 = 3 × 3 × 3 = 3³
• 100 = 10 × 10 = 10²

This is called the exponential notation. Any number raised to the power of 1 is the number itself (e.g., 7¹ = 7), and any non-zero number raised to the power of 0 is 1 (e.g., 5⁰ = 1).

---

2. Laws of Exponents

The chapter introduces several laws that help simplify expressions involving exponents. These laws apply when the bases are the same or when exponents are manipulated. Here are the key laws:

a) Multiplication of Powers with the Same Base

If the bases are the same, add the exponents.

• Rule: aᵐ × aⁿ = aᵐ⁺ⁿ
• Example: 2³ × 2⁴ = 2³⁺⁴ = 2⁷ = 128
• Explanation: 2³ = 2 × 2 × 2 and 2⁴ = 2 × 2 × 2 × 2. Multiplying them gives 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁷.

b) Division of Powers with the Same Base

If the bases are the same, subtract the exponents.

• Rule: aᵐ ÷ aⁿ = aᵐ⁻ⁿ (where a ≠ 0)
• Example: 5⁴ ÷ 5² = 5⁴⁻² = 5² = 25
• Explanation: 5⁴ = 5 × 5 × 5 × 5 and 5² = 5 × 5. Dividing gives (5 × 5 × 5 × 5) ÷ (5 × 5) = 5 × 5 = 5².

c) Power of a Power

When a number with an exponent is raised to another power, multiply the exponents.

• Rule: (aᵐ)ⁿ = aᵐ×ⁿ
• Example: (3²)³ = 3²×³ = 3⁶ = 729
• Explanation: 3² = 9, and raising it to the power of 3 means 9 × 9 × 9 = 729, which is 3⁶.

d) Power of a Product

When a product is raised to a power, each factor is raised to that power.

• Rule: (a × b)ᵐ = aᵐ × bᵐ
• Example: (2 × 3)² = 2² × 3² = 4 × 9 = 36
• Explanation: (2 × 3) = 6, and 6² = 36. Alternatively, 2² = 4 and 3² = 9, so 4 × 9 = 36.

e) Power of a Quotient

When a fraction is raised to a power, both the numerator and denominator are raised to that power.

• Rule: (a/b)ᵐ = aᵐ / bᵐ (where b ≠ 0)
• Example: (2/5)² = 2² / 5² = 4/25
• Explanation: 2² = 4 and 5² = 25, so (2/5)² = 4/25.

f) Zero Exponent Rule

Any non-zero number raised to the power of 0 is 1.

• Rule: a⁰ = 1 (where a ≠ 0)
• Example: 7⁰ = 1, 10⁰ = 1
• Explanation: This rule ensures consistency in the laws of exponents.

g) Negative Exponents

A number with a negative exponent is the reciprocal of the number with a positive exponent.

• Rule: a⁻ᵐ = 1/aᵐ (where a ≠ 0)
• Example: 2⁻³ = 1/2³ = 1/8
• Explanation: 2³ = 8, so 2⁻³ = 1/8.

---

3. Standard Form (Scientific Notation Exponents and Powers)

Large or small numbers can be expressed using powers of 10 in standard form. This is useful in science for handling numbers like distances between planets or sizes of atoms.

• Standard Form: A number is written as a × 10ⁿ, where 1 ≤ a < 10 and n is an integer.
• Example:
  • 5,600 = 5.6 × 10³ (Move decimal 3 places left)
  • 0.007 = 7 × 10⁻³ (Move decimal 3 places right)

Steps to convert:

1. Move the decimal point so that the number becomes between 1 and 10.
2. Count the number of places moved. If moved left, the exponent is positive; if moved right, it’s negative.
3. Write it as a × 10ⁿ.

---

4. Expressing Large Numbers in Exponential Form Exponents and Powers

The chapter teaches how to express large numbers using exponents, especially powers of 10.

• Example: 1,000 = 10³, 1,00,000 = 10⁵
• Application: The distance to the sun is about 149,600,000 km. In standard form, it’s 1.496 × 10⁸ km.

---

5. Solved Examples of Exponents and Powers

Here are some examples to illustrate the concepts:

Example 1: Simplify 2³ × 2⁵

• Solution: Using aᵐ × aⁿ = aᵐ⁺ⁿ, 2³ × 2⁵ = 2³⁺⁵ = 2⁸ = 256.

Example 2: Simplify (5²)³

• Solution: Using (aᵐ)ⁿ = aᵐ×ⁿ, (5²)³ = 5²×³ = 5⁶ = 15,625.

Example 3: Simplify 7⁴ ÷ 7²

• Solution: Using aᵐ ÷ aⁿ = aᵐ⁻ⁿ, 7⁴ ÷ 7² = 7⁴⁻² = 7² = 49.

Example 4: Write 0.00045 in standard form.

• Solution: Move decimal 4 places right to get 4.5. So, 0.00045 = 4.5 × 10⁻⁴.

Example 5: Simplify (2/3)³

• Solution: Using (a/b)ᵐ = aᵐ / bᵐ, (2/3)³ = 2³ / 3³ = 8/27.

---

6. Key Points to Remember: Exponents and Powers

• Exponents simplify repeated multiplication.
• Use the laws of exponents to combine or simplify expressions.
• Zero exponent rule: a⁰ = 1 (a ≠ 0).
• Negative exponents indicate reciprocals.
• Standard form uses powers of 10 for large or small numbers.

---

7. Practical Applications:Exponents and Powers

• Science: Exponents express distances (e.g., 3 × 10⁸ m/s for the speed of light).
• Finance: Compound interest uses exponential growth.
• Technology: Computer memory sizes (e.g., 2¹⁰ = 1024 bytes).

---

8. Practice Questions of Exponents and Powers

1. Simplify: 3⁴ × 3²
2. Find: (4³)²
3. Express 720 in exponential form.
4. Write 0.000089 in standard form.
5. Simplify: 5⁻²

Download pdf notes and Sulutions of the Chapter:

Chapter 14: Symmetry

Please Visit Readspot for Hindi Medium Study Material