Chapter 7: Fractions – Mathemetics

 

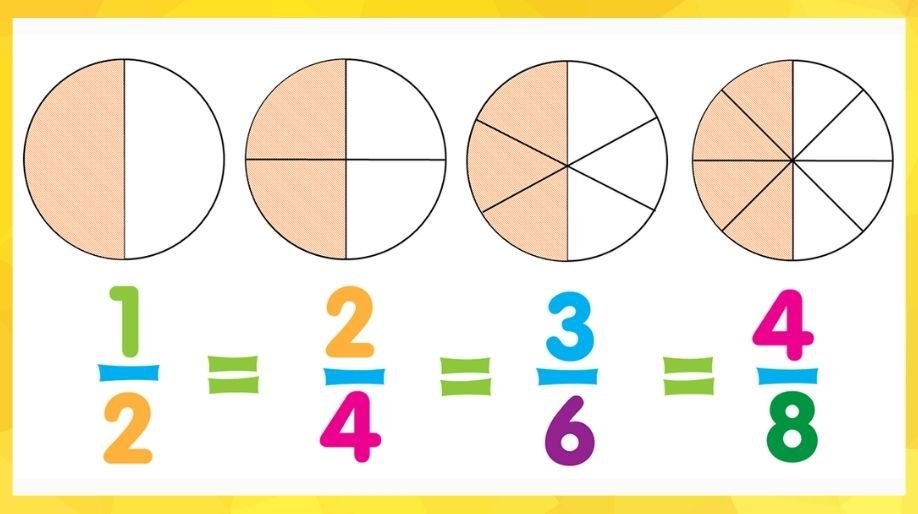
Fractions:

Fractions are an essential concept in mathematics, used to represent parts of a whole. Chapter 7 of Class 6 Maths focuses on understanding, comparing, and performing operations with fractions. Below are comprehensive notes on this chapter:

1. What is a Fraction?

A fraction represents a part of a whole. It is written in the form a/b, where:

• a is the numerator (the part considered).
• b is the denominator (the total number of equal parts).

Examples:

• 1/2 represents one part of a whole divided into two equal parts.
• 3/4 represents three parts of a whole divided into four equal parts.

Key Terms:

• Proper Fraction: The numerator is less than the denominator (e.g., 3/5).
• Improper Fraction: The numerator is greater than or equal to the denominator (e.g., 7/4).
• Mixed Fraction: A combination of a whole number and a proper fraction (e.g., 2 1/3).

2. Types of Fraction.

1. Like Fraction: Fraction with the same denominator (e.g., 1/7, 3/7, 5/7).
2. Unlike Fraction: Fraction with different denominators (e.g., 1/4, 2/5, 3/8).
3. Equivalent Fraction: Fraction that represent the same value but have different numerators and denominators (e.g., 1/2 = 2/4 = 4/8).

How to Find Equivalent Fractions:

Multiply or divide both the numerator and the denominator by the same non-zero number. For example:

• Multiply 1/3 by 2: .

3. Representation of Fractions

Fraction can be represented visually and on a number line:

a. Visual Representation:

A fraction can be shown using shaded portions of a shape, such as a circle or rectangle. For example:

• To represent 3/4, divide a rectangle into 4 equal parts and shade 3 of them.

b. Number Line Representation:

To represent fractions on a number line:

1. Divide the segment between 0 and 1 into equal parts based on the denominator.
2. Mark the numerator’s position on the number line.

Example: For 3/5, divide the line between 0 and 1 into 5 equal parts. Mark the third part.

4. Simplification of Fraction

To simplify a fraction:

1. Find the greatest common divisor (GCD) of the numerator and denominator.
2. Divide both by the GCD.

Example: Simplify 12/16:

• GCD of 12 and 16 is 4.
• Divide both by 4: .

5. Comparing Fraction:

a. Like Fraction:

Compare the numerators directly. The fraction with the larger numerator is greater.

Example: Compare 3/7 and 5/7:

• Since 5 > 3, .

b. Unlike Fraction:

Convert them to like fraction by finding a common denominator, then compare the numerators.

Example: Compare 2/3 and 3/4:

1. Find the least common denominator (LCD): .
2. Convert: and .
3. Compare: , so .

6. Addition and Subtraction of Fraction

a. Like Fraction:

Add or subtract the numerators while keeping the denominator the same.

Example: .

b. Unlike Fraction:

1. Convert to like fractions by finding a common denominator.
2. Add or subtract the numerators.

Example: :

1. LCD = 12.
2. Convert: , .
3. Add: .

7. Multiplication of Fraction:

To multiply two fractions:

1. Multiply the numerators.
2. Multiply the denominators.

Example: .

Multiplication with Whole Numbers:

Convert the whole number into a fraction with denominator 1 and then multiply.

Example: .

8. Division of Fraction:

To divide fraction:

1. Take the reciprocal of the divisor.
2. Multiply the fraction.

Example: :

1. Reciprocal of 2/5 is 5/2.
2. Multiply: .

9. Conversion of Fraction:

a. Mixed Fraction to Improper Fraction:

Use the formula:

Example: Convert 2 3/4:

• .
• Improper fraction: .

b. Improper Fraction to Mixed Fraction:

Divide the numerator by the denominator. The quotient is the whole number, and the remainder is the numerator of the fractional part.

Example: Convert 17/5:

• remainder 2.
• Mixed fraction: .

10. Decimal Representation of Fraction:

To convert a fraction to a decimal, divide the numerator by the denominator.

Example: Convert 3/8:

• .

11. Word Problems on Fraction:

Word problems involve real-life scenarios where fraction are used. Steps to solve:

1. Read the problem carefully.
2. Identify the fractions involved.
3. Perform the required operations (addition, subtraction, multiplication, or division).
4. Simplify the answer, if necessary.

Example:

A rope of length 5/6 m is cut into two pieces. One piece is 1/3 m. What is the length of the other piece?

• Total length = 5/6.
• One piece = 1/3.
• Length of the other piece = .
• Convert to like fractions: , .
• Subtract: .
• Answer: The other piece is 1/2 m long.

12. Applications of Fraction:

Fractions are used in various real-life scenarios, such as:

• Cooking (e.g., measuring ingredients).
• Dividing objects (e.g., sharing a pizza).
• Financial calculations (e.g., dividing expenses).

13. Key Points to Remember

• A fraction represents a part of a whole.
• Simplify fraction whenever possible.
• Always convert to like fraction for addition or subtraction.
• Multiplication and division of fraction do not require a common denominator.
• Mixed fraction can be converted to improper fractions and vice versa.

By mastering these concepts, students can build a strong foundation in fractions, which is crucial for understanding advanced mathematical topics.

 

Download PDF Notes and Excercise solution of the Chapter.

 

Chapter 8: Decimals ( Best Solution )

Please Visit Readspot for Hindi Medium Study Material